Understanding Entropy and Knowledge Accumulation in Neural Networks

Posted by Dr Bouarfa Mahi on 18 Feb, 2025

Understanding Entropy and Knowledge Accumulation in Neural Networks

Abstract

In this article, we explore the concept of entropy in neural networks and its role in tracking the accumulation of knowledge during the forward pass. We introduce a simple neural network diagram and demonstrate how entropy can be calculated at each forward pass, reflecting the uncertainty in the model’s predictions. This approach emphasizes the importance of understanding the evolution of decision confidence over time. Furthermore, we present a practical implementation of the entropy tracking system using the z-domain mapping, offering insights into how entropy can guide the learning process in neural networks.

---

1. Introduction

In the field of artificial intelligence (AI), the concept of entropy plays a crucial role in understanding the uncertainty and information contained in a model’s predictions. As AI systems evolve, they accumulate knowledge, which can be tracked through entropy. The reduction of entropy is often seen as an indicator of a model’s increasing decision confidence. However, this relationship is not always easy to visualize and quantify.

In this article, we present a simple neural network example with one hidden layer and one output neuron. We compute the entropy at each forward pass, which allows us to track how the model’s uncertainty decreases over time. The central idea is that the accumulation of knowledge in the model is reflected by a decreasing entropy value, corresponding to more structured decision-making. We also introduce a method for implementing entropy tracking using the z-domain, a unifying framework for knowledge accumulation.

---

2. The Neural Network Model

Consider a simple neural network with the following components:

• Input Layer: A set of $n$ input neurons, each representing a feature in the data.
• Hidden Layer: One layer with a single output neuron.
• Output Layer: A single output neuron denoted as $z_k$, representing the model’s prediction for the given input.

The forward pass in this network can be computed as:

$$ z_k = \left( \sum_{j=1}^{n} (w_{1,j} + G_{1,j}) x_j^{(0)} + b_1^{(0)} \right) $$

$$ D_k = \sigma \left(z_k\right) $$

Where:

• $x_j^{(0)}$ represents the inputs at the first layer (layer 0),
• $w_{1,j}$ represents the weights connecting the input layer to the output neuron,
• $b_1^{(0)}$ is the bias term,
• $D_k$ is the decision probability, and
• $\sigma$ is the activation function.

This equation gives the output of the model, $z_{k}$, for a given input.

---

3. Entropy Calculation

Entropy, $H(z)$, is a measure of the uncertainty or lack of structure in the model’s predictions. It is computed based on the output of the neural network at each forward pass. For a given output $z_k$, the entropy can be calculated as follows:

$$ H(z)|_k = - \frac{1}{\ln 2} \sum_{f=1}^{k} \left( z_f\, \Delta D_f \right) $$ $$ \Delta D_f = D_f - D_{f-1} $$

Where:

• $z_f$ represents the output at step $f$,
• $\Delta D_f$ is the change in the decision function associated with $z_f$.

The entropy value reflects how much uncertainty is present in the network's predictions. As the model learns and accumulates knowledge, entropy decreases, which indicates that the network is becoming more confident in its predictions. This process can be observed after each forward pass as the entropy value is updated.

3.1 Example with a Simple Neural Network

The neural network shown in the diagram below calculates the entropy at each forward pass. The input layer consists of 5 neurons, and the output layer has a single neuron, denoted as $z_k$. After each forward pass, the entropy is calculated using the formula provided above, and the resulting value is updated to reflect the increasing confidence of the network.

• 

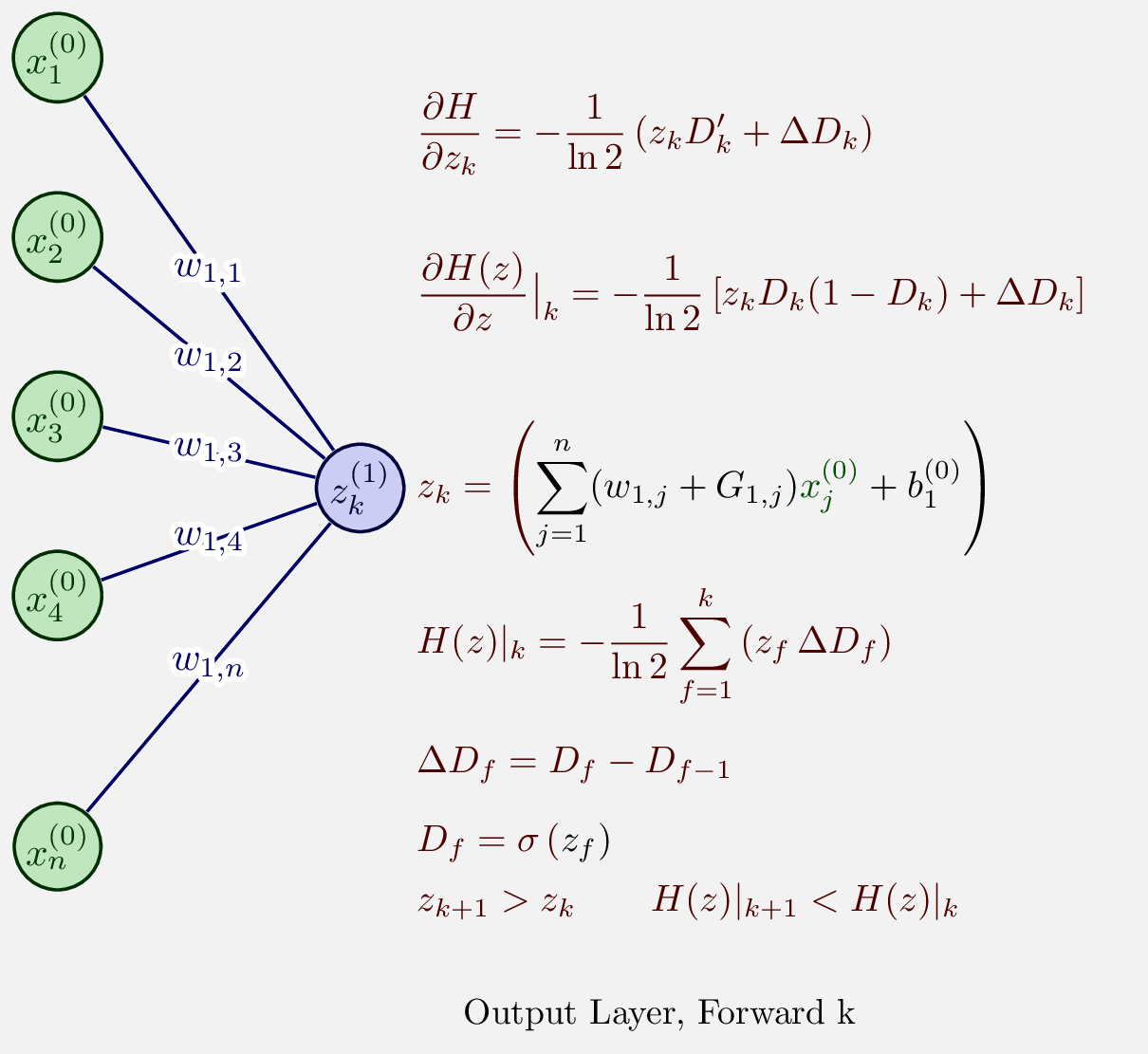
In this network, we track the entropy after each forward pass to see how the uncertainty in the model’s predictions decreases as it learns.

---

4. The Role of the z-Domain in Knowledge Accumulation

The z-domain serves as a unified framework for modeling the accumulation of knowledge in AI systems. By mapping raw input data into a cumulative representation, the z-domain tracks how knowledge evolves over time. Each step $z_k$ corresponds to a measurable increase in knowledge, and the overall knowledge state is represented by the cumulative sum:

$$ z_k = z_0 + \sum_{f=1}^{k} \Delta y_f $$

Where:

• $\Delta y_f$ represents the incremental knowledge gained at each step.

In this framework, the z-domain provides a natural progression of knowledge accumulation. By monitoring how $z_k$ evolves, we can track the learning process and measure how well the model is acquiring structured knowledge.

4.1 Dynamic Learning Rate Adjustment

To ensure that the knowledge accumulation process is smooth and controlled, we introduce a dynamic learning rate adjustment mechanism. This mechanism ensures that the updates to the network’s weights produce positive and bounded increases in knowledge. The learning rate, $\eta$, is adjusted such that the updates lead to:

1. A monotonic increase in $z$, ensuring that knowledge accumulates over time.
2. A bounded increment, meaning that the change in knowledge between successive steps is controlled to avoid sudden jumps in knowledge accumulation.

This dynamic adjustment helps ensure that the network's learning process is gradual and consistent for the discrete case:

$$ \frac{\partial H(z)}{\partial z} \big|_k = -\frac{1}{\ln 2} \left[ z_k D_k (1 - D_k) + \Delta D_k \right] $$

$$ \frac{\partial H}{\partial w_{ij}}|_k = \frac{\partial H(z)}{\partial z}|_k \cdot x_j $$

$$ \frac{\partial H}{\partial G_{ij}}|_k = \frac{\partial H(z)}{\partial z}|_k \cdot x_j $$

$$ \frac{\partial H}{\partial b_{i}}|_k = \frac{\partial H(z)}{\partial z}|_k $$

The update rules are:

$$ w_{ij} \leftarrow w_{ij} - \eta \frac{\partial H}{\partial w_{ij}}|_k $$

$$ G_{ij} \leftarrow G_{ij} - \eta \frac{\partial H}{\partial G_{ij}}|_k $$

$$ b_i \leftarrow b_i - \eta \frac{\partial H}{\partial b_i}|_k $$

where $\eta$ is the learning rate.

---

5. Conclusion

This article introduces a method for tracking entropy in neural networks, offering insights into the process of knowledge accumulation. By calculating entropy at each forward pass and updating it dynamically, we can monitor how the network's predictions evolve and become more structured over time. The z-domain framework allows for a unified representation of knowledge accumulation, ensuring that the learning process is gradual and controlled.

Through the combination of entropy calculation and the z-domain framework, we can gain a deeper understanding of the model's decision-making process, providing a valuable tool for building adaptive, efficient, and interpretable AI systems. This approach offers a new way to think about the intersection of knowledge, uncertainty, and decision-making, which could have profound implications for future AI development.

ENTROPY KNOWLEDGE   

---