Blog
Structured Knowledge Accumulation: An Autonomous Framework for Layer-Wise Entropy Reduction in Neural Learning
Posted by Dr Bouarfa Mahi
on 25 Feb, 2025
February 2025
DOI: 10.13140/RG.2.2.35390.80963
License CC BY-NC-ND 4.0
Abstract
We introduce the Structured Knowledge Accumulation (SKA) framework, which redefines entropy as a dynamic, layer-wise measure of knowledge alignment in neural networks: $H^{(l)} = -\frac{1}{\ln 2} \sum_{k=1}^{K} \mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k$, where $\mathbf{z}^{(l)}_k$ is the knowledge vector and $\Delta \mathbf{D}^{(l)}_k$ is the decision probability shift vector at layer $l$ over $K$ forward steps. Rooted in the continuous entropy formulation $H = -\frac{1}{\ln 2} \int z \, dD$, SKA derives the sigmoid function, $D_i^{(l)} = \frac{1}{1 + e^{-z_i^{(l)}}}$, as an emergent property of entropy minimization. This approach generalizes to fully connected networks without backpropagation, with each layer optimizing locally by aligning $\mathbf{z}^{(l)}_k$ with $\Delta \mathbf{D}^{(l)}_k$, guided by $\cos(\theta^{(l)}_{k})$. Total network entropy, $H = \sum_{l=1}^{L} H^{(l)}$, decreases hierarchically as knowledge structures evolve. Offering a scalable, biologically plausible alternative to gradient-based training, SKA bridges information theory and artificial intelligence, with potential applications in resource-constrained and parallel computing environments.
1. Introduction
Entropy, classically defined by Shannon1 as
$H = -\sum p_i \log_2 p_i$, quantifies uncertainty in a static, discrete
probabilistic system. While foundational, this formulation falls short
of capturing the dynamic, continuous structuring of knowledge in
intelligent systems like neural networks. The sigmoid function,
$\sigma(z) = \frac{1}{1 + e^{-z}}$, a cornerstone of artificial
intelligence (AI), has lacked a theoretical basis beyond empirical
utility. Conventional training via backpropagation, which propagates
errors backward through the network, is computationally intensive and
biologically implausible, constraining scalability and real-world
applicability.
This article presents the Structured Knowledge Accumulation (SKA)
framework, reimagining entropy as a continuous process of knowledge
accumulation. We propose:
-
Entropy as a dynamic measure, expressed in layers as
$H^{(l)} = -\frac{1}{\ln 2} \sum_{k=1}^{K} \mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k$,
approximating the continuous $H = -\frac{1}{\ln 2} \int z \, dD$,
-
Structured knowledge ($z$) and its continuous accumulation as the
foundation of learning,
-
A forward-only, backpropagation-free learning rule driven by local
entropy minimization.
We derive the sigmoid from continuous entropy reduction, extend it to
fully connected networks, and demonstrate learning through local
alignment of knowledge with decision dynamics. This framework offers a
novel perspective for AI, enhancing optimization efficiency,
interpretability, and biological plausibility, with implications for
scalable and distributed neural systems.
2. Redefining Entropy in the SKA Framework
Entropy traditionally quantifies uncertainty in probabilistic systems,
but its classical form is static and discrete, limiting its
applicability to dynamic learning processes like those in neural
networks. In the Structured Knowledge Accumulation (SKA) framework, we
redefine entropy as a continuous, evolving measure that reflects
knowledge alignment over time or processing steps. This section
contrasts Shannon's discrete entropy with our continuous reformulation,
enabling the use of continuous decision probabilities and supporting the
derivation of the sigmoid function through entropy minimization.
2.1 Classical Shannon Entropy
For a binary system with decision probability $D$, Shannon's entropy is:
$$
\tag{1}
H = -D \log_2 D - (1 - D) \log_2 (1 - D)
$$
Its derivative with respect to $D$ is:
$$
\tag{2}
\frac{dH}{dD} = \log_2 \left( \frac{1 - D}{D} \right)
$$
This formulation assumes $D$ is a fixed probability, typically
associated with discrete outcomes (e.g., 0 or 1). While foundational, it
does not capture the continuous evolution of knowledge in a learning
system, where $D$ may vary smoothly as the network processes inputs. To
address this, we seek a continuous entropy measure that accommodates
dynamic changes in $D$, aligning with the SKA's focus on knowledge
accumulation.
2.2 Entropy as Knowledge Accumulation
In SKA, we redefine entropy for a single neuron as a continuous process:
$$
\tag{3}
H = -\frac{1}{\ln 2} \int z \, dD
$$
Here, $z$ represents the neuron's
structured knowledge, and $dD$ is an infinitesimal change in the
decision probability, treated as a continuous variable over the range
$[0, 1]$. The factor $-\frac{1}{\ln 2}$ ensures alignment with base-2
logarithms, consistent with Shannon's information units. Unlike the
static snapshot of Equation 1, this integral captures how entropy
accumulates as $z$ drives changes in $D$, reflecting a dynamic learning
process.
For a layer $l$ with $n_l$ neurons over $K$ forward steps, we
approximate this continuous form discretely:
$$
\tag{4}
H^{(l)} = -\frac{1}{\ln 2} \sum_{k=1}^{K} \mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k
$$
where $\mathbf{z}^{(l)}_k = [z_1^{(l)}(k), \dots, z_{n_l}^{(l)}(k)]^T$
is the knowledge vector,
$\Delta \mathbf{D}^{(l)}_k = [\Delta D_1^{(l)}(k), \dots, \Delta D_{n_l}^{(l)}(k)]^T$
is the vector of decision probability shifts, and the scalar product is:
$$
\tag{5}
\mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k = \sum_{i=1}^{n_l} z_i^{(l)}(k) \Delta D_i^{(l)}(k)
$$
The total network entropy sums over all layers:
$$
\tag{6}
H = \sum_{l=1}^{L} H^{(l)}
$$
Equation 3 is the core theoretical
construct, with Equation 4 as its practical discrete approximation. As
$K \to \infty$ and $\Delta \mathbf{D}^{(l)}_k$ becomes infinitesimally
small, Equation 4 approaches the continuous integral, enabling us to
model $D$ as a smooth function of $z$. This continuous perspective is
essential for deriving the sigmoid using dynamics in later sections,
while the discrete form supports implementation in neural architectures.
2.3 Accumulated Knowledge
Knowledge accumulates over steps:
$$
\tag{7}
z_k = z_0 + \sum_{f=1}^{k} \Delta z_f
$$
In a layer,
$\mathbf{z}^{(l)}_k$ evolves, reducing $H^{(l)}$ as it aligns with
$\Delta \mathbf{D}^{(l)}_k$.
3. Deriving the Sigmoid Function
The SKA framework posits that the sigmoid function emerges naturally
from continuous entropy minimization, linking structured knowledge to
decision probabilities. This section demonstrates that when $D$ follows
$D = \frac{1}{1 + e^{-z}}$, the SKA entropy $H_{\text{SKA}}$ equals the
classical Shannon entropy $H_{\text{Shannon}}$, differing by a constant
(zero). By leveraging the continuous formulation from Section 2, we
derive this equivalence, reinforcing the framework's theoretical
grounding.
3.1 Key Definitions
3.1.1 Shannon Entropy (for binary decisions)
For a binary system with continuous decision probability $D$:
$$
\tag{8}
H_{\text{Shannon}} = -D \log_2 D - (1-D) \log_2 (1-D)
$$
3.1.2 SKA Entropy (layer-wise, for a single neuron)
The SKA entropy, defined continuously as in Section 2.2, is:
$$
\tag{9}
H_{\text{SKA}} = -\frac{1}{\ln 2} \int z \, dD,
$$
where
$z = -\ln\left(\frac{1-D}{D}\right)$ relates knowledge to $D$,
consistent with $D = \frac{1}{1 + e^{-z}}$ as shown in Section 3.1.
3.2 Equivalence Proof
Substituting $z = -\ln\left(\frac{1-D}{D}\right)$ (or equivalently,
$z = \ln\left(\frac{D}{1-D}\right)$) into $H_{\text{SKA}}$:
$$
\tag{10}
H_{\text{SKA}} = -\frac{1}{\ln 2} \int \ln\left(\frac{D}{1-D}\right) dD.
$$
Evaluate the integral with substitution $u = D$, $du = dD$:
$$
\tag{11}
\int \ln\left(\frac{D}{1-D}\right) dD = D \ln\left(\frac{D}{1-D}\right) + \ln(1-D).
$$
Substituting back:
$$
\tag{12}
H_{\text{SKA}} = -\frac{1}{\ln 2} \left[ D \ln\left(\frac{D}{1-D}\right) + \ln(1-D) \right].
$$
Rewrite $\ln\left(\frac{D}{1-D}\right) = \ln D - \ln(1-D)$:
$$
\tag{13}
H_{\text{SKA}} = -\frac{1}{\ln 2} \left[ D \ln D - D \ln(1-D) + \ln(1-D) \right].
$$
Factorize:
$$
\tag{14}
H_{\text{SKA}} = -\frac{1}{\ln 2} \left[ D \ln D + (1-D) \ln(1-D) \right].
$$
Thus:
$$
\tag{15}
H_{\text{SKA}} = H_{\text{Shannon}}.
$$
3.3 Implications
-
Zero Difference: The SKA and Shannon entropies are identical
(differing by zero) when $D = \frac{1}{1 + e^{-z}}$, confirming the
sigmoid as an emergent property of continuous entropy reduction.
-
Knowledge Alignment: This equivalence stems from $z$ structuring
$D$ to minimize uncertainty, as defined in Sections 2 and 3.
3.4 Significance
-
Theoretical Consistency: SKA extends Shannon entropy into a
continuous, dynamic context while preserving its core properties for
sigmoidal outputs.
-
Backpropagation-Free Learning: Since
$H_{\text{SKA}} = H_{\text{Shannon}}$, layer-wise entropy
minimization aligns with classical uncertainty reduction, achieved
via forward dynamics alone.
-
Biological Plausibility: The continuous, local alignment of $z$
with $D$ mirrors plausible neural learning mechanisms.
3.5 Summary
When $D$ is the sigmoid function, $H_{\text{SKA}}$ matches
$H_{\text{Shannon}}$ exactly, with a difference of zero. This result,
derived from the continuous entropy
$H_{\text{SKA}} = -\frac{1}{\ln 2} \int z \, dD$, validates SKA's
foundation and its seamless integration with information theory,
leveraging continuous dynamics for neural learning with classical
information theory.
4 The Fundamental Law of Entropy Reduction
The SKA framework establishes a fundamental law governing how entropy
decreases as structured knowledge evolves. This section derives this law
using continuous dynamics, reflecting the continuous nature of decision
probabilities and knowledge accumulation introduced in Sections 2 and 3.
We then provide a discrete approximation for practical implementation,
ensuring the framework's applicability to neural networks while rooting
it in a continuous theoretical foundation.
4.1 Continuous Dynamics
For a single neuron, the rate of entropy change with respect to
structured knowledge $z$ is derived from the continuous entropy
$H = -\frac{1}{\ln 2} \int z \, dD$. Taking the partial derivative:
$$
\tag{16}
\frac{\partial H}{\partial z} = -\frac{1}{\ln 2} z D (1 - D)
$$
This
follows from $D = \frac{1}{1 + e^{-z}}$ (as derived in Section 4), where
$\frac{dD}{dz} = D (1 - D)$, and reflects the neuron's local
contribution to entropy reduction. For a layer $l$ with $n_l$ neurons at
step $k$, this extends to each neuron $i$:
$$
\tag{17}
\frac{\partial H^{(l)}}{\partial z_i^{(l)}(k)} = -\frac{1}{\ln 2} z_i^{(l)}(k) D_i^{(l)}(k) \left(1 - D_i^{(l)}(k)\right)
$$
Equation 17 governs the continuous reduction of layer-wise entropy
$H^{(l)}$, driven by the alignment of $z_i^{(l)}(k)$ with the sigmoidal
decision probability $D_i^{(l)}(k)$. This dynamic, localized process
underpins the SKA's forward-only learning mechanism, leveraging the
continuous evolution of $D$ over time or input processing.
4.2 Discrete Dynamics
In practice, neural networks operate over discrete forward steps. For a
single neuron at step $k$, the entropy gradient approximates the
continuous form, incorporating the change in decision probability
$\Delta D_k = D_k - D_{k-1}$:
$$
\tag{18}
\frac{\partial H}{\partial z} \big|_k = -\frac{1}{\ln 2} \left[ z_k D_k (1 - D_k) + \Delta D_k \right]
$$
For layer $l$ at step $k$, this becomes:
$$
\tag{19}
\frac{\partial H^{(l)}}{\partial z_i^{(l)}(k)} = -\frac{1}{\ln 2} z_i^{(l)}(k) \left[ D_i^{(l)}(k) \left(1 - D_i^{(l)}(k)\right) + \Delta D_i^{(l)}(k) \right]
$$
Equation 19 adapts the continuous law to discrete steps, where
$\Delta D_i^{(l)}(k)$ captures the step-wise shift in $D_i^{(l)}(k)$.
While Equation 17 represents the ideal continuous dynamics, Equation 19
provides a computable approximation, aligning knowledge adjustments with
observed changes in decision probabilities across discrete iterations.
5 Generalization to Fully Connected Networks
The SKA framework extends seamlessly from single neurons to fully
connected neural networks, leveraging the continuous entropy reduction
principles established earlier. For a network with $L$ layers, knowledge
and decision probabilities evolve hierarchically, reducing total entropy
through local, forward-only adjustments. This section outlines how SKA
operates across layers, maintaining its biologically plausible and
scalable design.
For a network with $L$ layers:
-
$\mathbf{z}^{(l)}_k = \mathbf{W}^{(l)} \mathbf{x}^{(l-1)}_k + \mathbf{b}^{(l)}$,
the knowledge vector at layer $l$ and step $k$,
-
$\mathbf{D}^{(l)}_k = \sigma(\mathbf{z}^{(l)}_k)$, the decision
probabilities derived via the sigmoid function,
-
$\Delta \mathbf{D}^{(l)}_k = \mathbf{D}^{(l)}_k - \mathbf{D}^{(l)}_{k-1}$,
the step-wise shift in decision probabilities.
Layer-wise entropy, rooted in the continuous formulation, is
approximated discretely:
$$
\tag{20}
H^{(l)} = -\frac{1}{\ln 2} \sum_{k=1}^{K} \mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k
$$
The alignment between knowledge and decision shifts is quantified as:
$$
\tag{21}
\mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k = \|\mathbf{z}^{(l)}_k\| \| \Delta \mathbf{D}^{(l)}_k\| \cos(\theta^{(l)}_k)
$$
Total network entropy aggregates across layers:
$$
\tag{22}
H = \sum_{l=1}^{L} H^{(l)}
$$
Learning proceeds by aligning
$\mathbf{z}^{(l)}_k$ with $\Delta \mathbf{D}^{(l)}_k$ at each layer,
reducing $H^{(l)}$ locally without requiring backward error propagation.
In the continuous limit, this alignment reflects a smooth evolution of
knowledge, approximated here by discrete steps for computational
feasibility.
6 Learning Without Backpropagation
SKA achieves learning through localized entropy minimization,
eliminating the need for backpropagation by leveraging forward-only
dynamics. This section details the weight update mechanism and
supporting metrics, grounded in the continuous entropy reduction law,
and adapted for discrete implementation in fully connected networks.
Entropy minimization at layer $l$ is driven by:
$$
\tag{23}
\frac{\partial H^{(l)}}{\partial w_{ij}^{(l)}} = -\frac{1}{\ln 2} \sum_{k=1}^{K} \frac{\partial (\mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k)}{\partial w_{ij}^{(l)}}
$$
The update rule adjusts weights forward:
$$
\tag{24}
w_{ij}^{(l)} \leftarrow w_{ij}^{(l)} - \eta \frac{\partial H^{(l)}}{\partial w_{ij}^{(l)}}
$$
Here, $\Delta D_i^{(l)}(k)$ is computed directly from forward passes,
bypassing the need for error backpropagation. This local adjustment
aligns with the continuous dynamics of knowledge evolution, approximated
over discrete steps.
Step-wise Entropy Change
To quantify knowledge accumulation, the step-wise entropy change at
layer $l$ and step $k$ is:
$$
\tag{25}
\Delta H^{(l)}_k = H^{(l)}_k - H^{(l)}_{k-1} = -\frac{1}{\ln 2} \mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k
$$
This measures uncertainty reduction as $\mathbf{z}^{(l)}_k$ aligns with
$\Delta \mathbf{D}^{(l)}_k$, with total layer entropy as:
$$
\tag{26}
H^{(l)} = \sum_{k=1}^{K} \Delta H^{(l)}_k
$$
Entropy Gradient
The gradient of $H^{(l)}$ with respect to $\mathbf{z}^{(l)}_k$ at step
$k$ is:
$$
\tag{27}
\nabla H^{(l)} = \frac{\partial H^{(l)}}{\partial \mathbf{z}^{(l)}_k} = -\frac{1}{\ln 2} \mathbf{z}^{(l)}_k \odot \mathbf{D}'^{(l)}_k - \Delta \mathbf{D}_k^{(l)}
$$
where
$\mathbf{D}'^{(l)}_k = \mathbf{D}^{(l)}_k \odot (\mathbf{1} - \mathbf{D}^{(l)}_k)$
is the sigmoid derivative. This gradient guides updates to minimize
$H^{(l)}$, aligning knowledge with decision shifts.
Knowledge Evolution Across Layers
The gradient
$\nabla H^{(l)} = -\frac{1}{\ln 2} \mathbf{z}^{(l)}_k \odot \mathbf{D}'^{(l)}_k - \Delta \mathbf{D}_k^{(l)}$
drives entropy reduction in layer $l$ at step $k$. As
$\mathbf{D}^{(l-1)}_k$ feeds into $\mathbf{z}^{(l)}_k$, each layer
adapts uniquely---extracting broad features early and refining decisions
later---mirroring a continuous knowledge flow approximated discretely.
Governing Equation of SKA
The network evolves according to:
$$
\tag{28}
\nabla H^{(l)} + \frac{1}{\ln 2} \mathbf{z}^{(l)}_k \odot \mathbf{D}'^{(l)}_k + \Delta \mathbf{D}_k^{(l)} = 0
$$
where $\nabla H^{(l)}$ minimizes entropy layer-wise, with updates
following $-\nabla H^{(l)}$ to align $\mathbf{z}^{(l)}_k$ with
$\Delta \mathbf{D}^{(l)}_k$.
Inter-Layer Entropy Change
The entropy change between layers $l$ and $l+1$ at step $k$ is:
$$
\tag{29}
\Delta H^{(l,l+1)}_k = -\frac{1}{\ln 2} \left[ \mathbf{z}^{(l+1)}_k \cdot \Delta \mathbf{D}^{(l+1)}_k - \mathbf{z}^{(l)}_k \cdot \Delta \mathbf{D}^{(l)}_k \right]
$$
This quantifies the spatial evolution of knowledge, complementing the
temporal guidance of $\nabla H^{(l)}$, as entropy decreases through the
network.
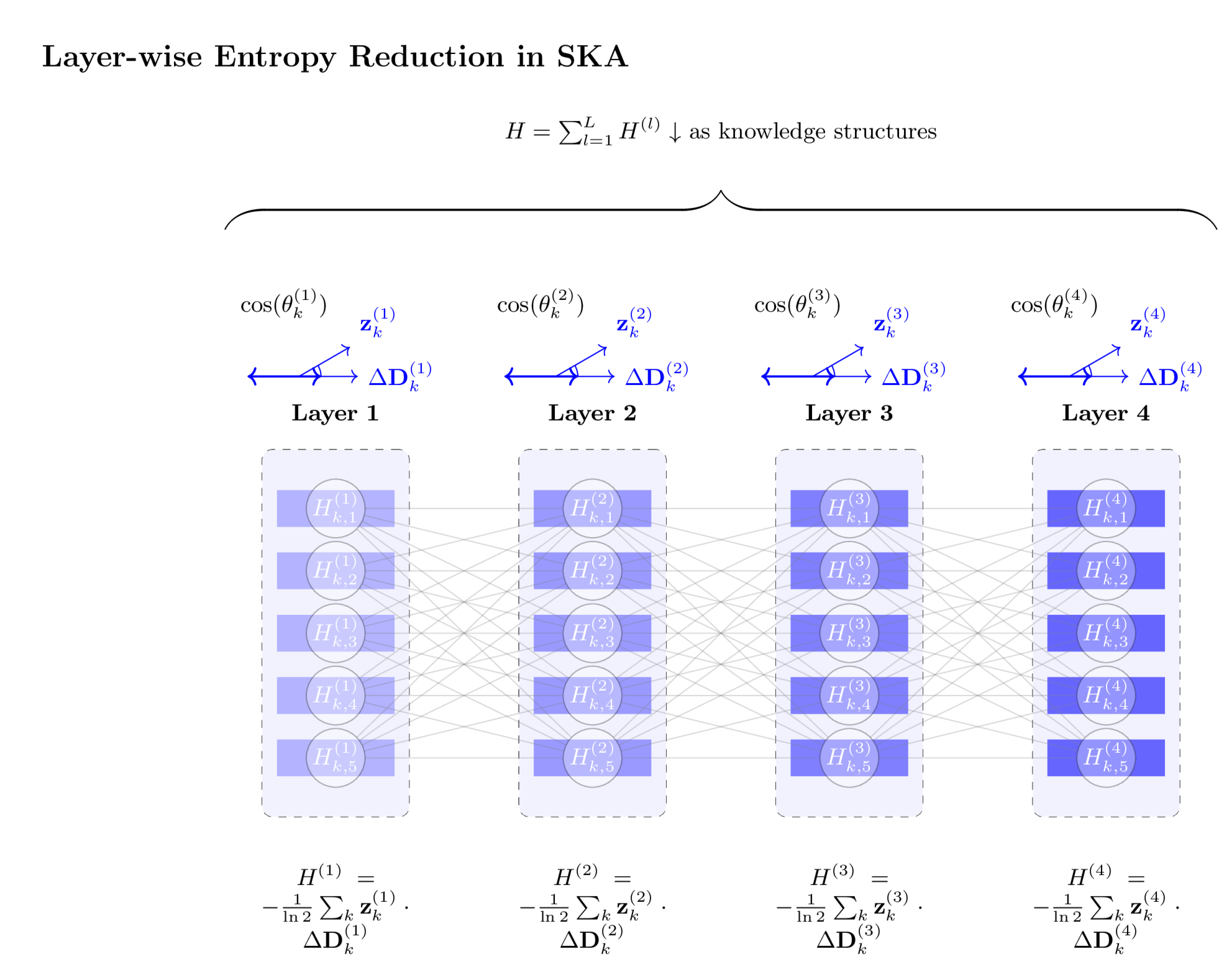
7 Application to Neural Networks
SKA structures knowledge hierarchically across layers, reducing total
entropy $H$ through continuous dynamics approximated over discrete
steps. A multilayer perceptron (MLP) can train by minimizing $H$, with
$\cos(\theta^{(l)}_k)$ serving as a practical metric to monitor
alignment between $\mathbf{z}^{(l)}_k$ and $\Delta \mathbf{D}^{(l)}_k$.
This forward-only process leverages the framework's scalability and
autonomy, applicable to diverse network architectures.
Layer-wise entropy reduction across layers at step $k$. Color intensity represents entropy level (darker blue = lower entropy), decreasing from Layer 1 to Layer 4. Each layer locally minimizes entropy by aligning knowledge vectors $\mathbf{z}^{(l)}_k$ with decision change vectors $\Delta \mathbf{D}^{(l)}_k$, measured by $\cos(\theta^{(l)}_k)$.
8 Tensor-Based Implementation of SKA
To enable efficient computation and scalability, we propose a tensor-based implementation of the Structured Knowledge Accumulation (SKA) framework. This approach maintains the theoretical foundation while optimizing operations for parallel computing.
Tensor Definitions
For a neural network with multiple layers, time steps, and neurons per layer, we define the following tensors:
- Knowledge Tensor ($\mathbf{Z}$): Represents structured knowledge across layers and steps. It has a shape of $[L, K, n_{\text{max}}]$, where:
- $L$ is the number of layers,
- $K$ is the number of forward steps,
- $n_{\text{max}}$ is the maximum number of neurons per layer.
-
Each element $\mathbf{Z}_{l,k,i}$ corresponds to the knowledge value of neuron $i$ in layer $l$ at step $k$.
-
Decision Probability Tensor ($\mathbf{D}$): Stores the output probabilities after applying the sigmoid function. It shares the same shape as $\mathbf{Z}$ and is computed as:
$$
\mathbf{D}_{l,k,i} = \sigma(\mathbf{Z}_{l,k,i})
$$
where $\sigma$ is the sigmoid function.
-
Shift Tensor ($\Delta \mathbf{D}$): Captures the change in decision probabilities between consecutive steps. It has a shape of $[L, K-1, n_{\text{max}}]$ and is defined as:
$$
\Delta \mathbf{D}_{l,k,i} = \mathbf{D}_{l,k+1,i} - \mathbf{D}_{l,k,i}
$$
-
Weight Tensor ($\mathbf{W}$): Stores the weights connecting neurons across layers. It has a shape of $[L, n_{\text{max}}, n_{\text{max}}]$, where each entry $\mathbf{W}_{l,i,j}$ represents the weight between neurons $i$ and $j$ in layer $l$.
-
Bias Tensor ($\mathbf{b}$): Contains biases for each neuron, with a shape of $[L, n_{\text{max}}]$, where each element $\mathbf{b}_{l,i}$ is the bias of neuron $i$ in layer $l$.
Knowledge Update Process
The structured knowledge tensor is computed using a weighted sum of inputs and biases:
$$
\mathbf{Z} = \mathbf{W} \cdot \mathbf{X} + \mathbf{b}
$$
where:
- $\mathbf{X}$ is the input tensor, which has the same shape as $\mathbf{Z}$,
- The first layer ($l=0$) receives direct inputs, while subsequent layers take the decision probability outputs from the previous layer.
Entropy Calculation
For each layer, entropy is computed using the following equation:
$$
\mathbf{H}_l = -\frac{1}{\ln 2} \sum_{k=1}^{K-1} \mathbf{Z}_{l,k+1,:} \cdot \Delta \mathbf{D}_{l,k,:}
$$
where $\mathbf{H}_l$ is a tensor of shape $[L]$, representing the entropy for each layer. The total entropy across the network is then:
$$
H = \sum_{l=1}^{L} \mathbf{H}_l
$$
Entropy Gradient for Learning
The gradient of entropy with respect to structured knowledge is given by:
$$
\nabla \mathbf{H} = -\frac{1}{\ln 2} \mathbf{Z}_{:,1:K,:} \odot \mathbf{D}' + \Delta \mathbf{D}
$$
where:
- $\mathbf{D}'$ is the derivative of the sigmoid function:
$$
\mathbf{D}' = \mathbf{D}_{:,1:K,:} \odot (1 - \mathbf{D}_{:,1:K,:})
$$
Weight Updates
To minimize entropy, the weight tensor is updated using:
$$
\mathbf{W} \leftarrow \mathbf{W} - \eta \frac{\partial \mathbf{H}}{\partial \mathbf{W}}
$$
where $\eta$ is the learning rate.
Monitoring Learning Progress
To track alignment between knowledge and decision probability shifts, we define an alignment tensor:
$$
\Theta_{l,k} = \cos(\theta^{(l)}_{k+1}) = \frac{\mathbf{Z}_{l,k+1,:} \cdot \Delta \mathbf{D}_{l,k,:}}{\|\mathbf{Z}_{l,k+1,:}\| \|\Delta \mathbf{D}_{l,k,:}\|}
$$
This tensor helps evaluate whether knowledge accumulation is following the expected trajectory.
Advantages of Tensor Implementation
- Efficient Computation: Tensor operations allow parallel processing across layers and neurons.
- Scalability: The implementation can handle large-scale models without excessive computational overhead.
- Simplified Learning: Updates occur simultaneously for all neurons and layers, reducing complexity.
This tensor-based SKA implementation ensures that structured knowledge accumulation is efficient, scalable, and computationally optimized.
9 Implications and Future Work
The SKA framework offers transformative potential for neural network
design and application, rooted in its continuous entropy reduction
principles. Key implications and research directions include:
-
Autonomous Learning: Layers independently minimize entropy,
enabling self-sufficient training without global coordination.
-
Decentralization: Local updates allow distribution across
separate hardware, enhancing scalability in parallel systems.
-
Efficiency: Forward-only learning reduces memory demands
compared to backpropagation-based methods.
-
Interpretability: Monitoring $\cos(\theta^{(l)}_k)$ provides
insight into layer-wise knowledge alignment.
-
Experiments: Future work will compare SKA's performance to
stochastic gradient descent (SGD) on datasets like MNIST, validating
its efficacy.
-
Real-Time Processing: Single-pass updates suit SKA for
processing live data streams efficiently.
10 Conclusion
The SKA framework reimagines neural networks as systems that structure
knowledge to minimize entropy, deriving the sigmoid function from
continuous first principles and eliminating backpropagation. By
leveraging local, forward-only dynamics, SKA offers a scalable,
biologically inspired paradigm for AI, bridging information theory and
neural learning with broad applicability.
Reference
- C. E. Shannon, "A Mathematical Theory of Communication," Bell System
Technical Journal, vol. 27, pp. 379--423, 1948.
SKA NEURAL NETWORK FRAMEWORK